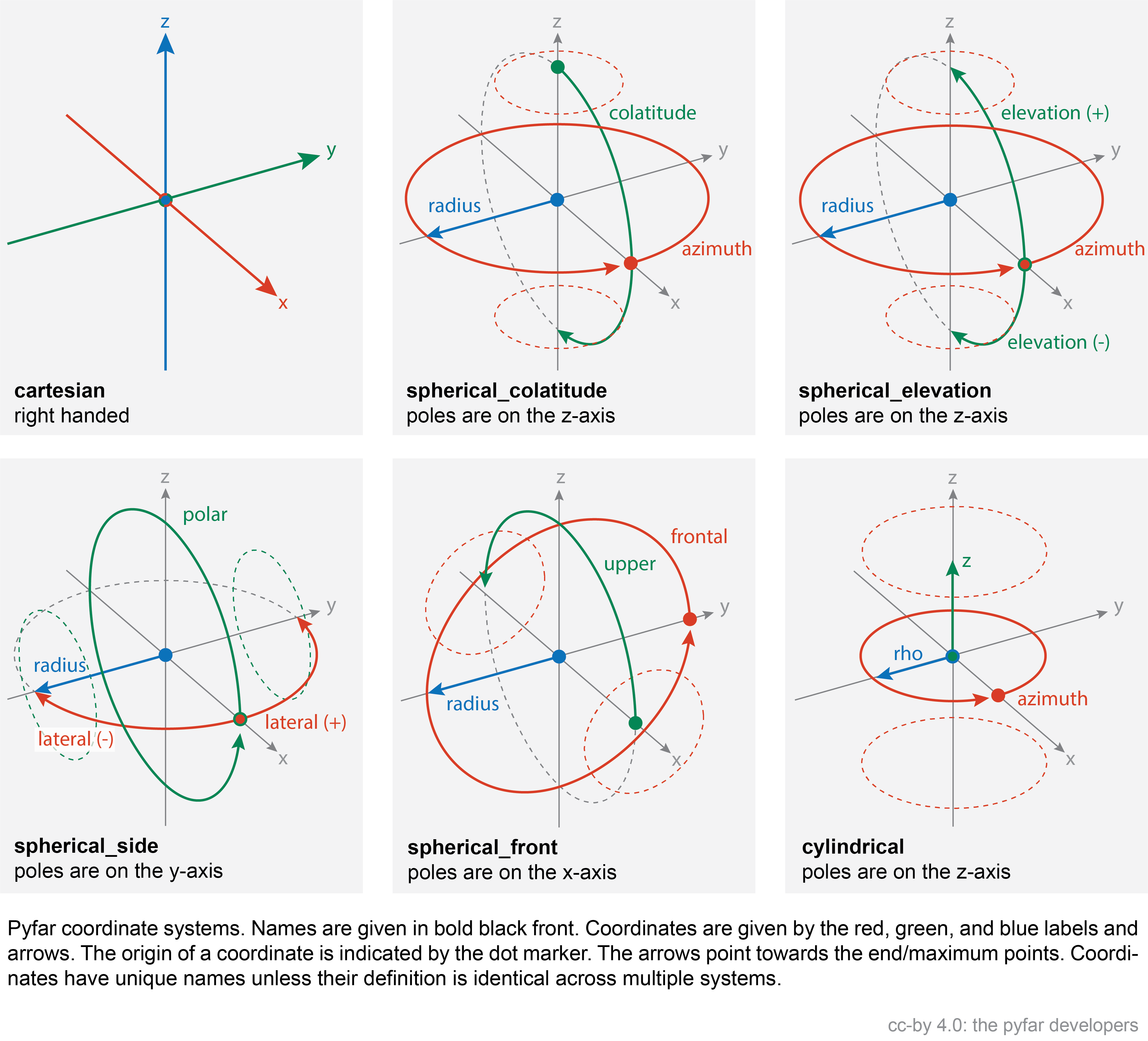
Coordinates#

The following introduces the Coordinates class and the coordinate systems that are available in pyfar. Available sampling schemes are listed at spharpy.samplings. Examples for working with Coordinates objects are part of the pyfar gallery.

Different coordinate systems are frequently used in acoustics research and handling sampling points and different systems can be cumbersome. The Coordinates class was designed with this in mind. It stores coordinates in cartesian coordinates internally and can convert to all coordinate systems listed below. Additionally, the class can query and plot coordinates points. Addition and subtraction are supported with numbers and Coordinates objects, while multiplication and division are supported with numbers only. All arithmetic operations are performed element-wise on Cartesian coordinates using the appropriate operator. Functions for converting coordinates not stored in a Coordinates object are available for convenience. However, it is strongly recommended to use the Coordinates class for all conversions.

Coordinate Systems#

Each coordinate system has a unique name, e.g., spherical_elevation, and is defined by three coordinates, in this case azimuth, elevation, and radius. The available coordinate systems are shown in the image below.

Coordinates#

The unit for length for the coordinates is always meter, while the unit for angles is radians. Each coordinate is unique, but can appear in multiple coordinate systems, e.g., the azimuth angle is contained in two coordinate systems (spherical_colatitude and spherical_elevation). The table below lists all coordinates.

Note

All coordinates are returned as copies of the internal data. This means that for example coordinates.x[0] = 0 does not change coordinates.x. This can be done using

new_x = coordinates.x
new_x[0] = 0
coordinates.x = new_x

Coordinate	Descriptions
`x`, `y`, `z`	x, y, z coordinate of a right handed Cartesian coordinate system in meter (\(-\infty\) < x,y,z < \(\infty\)).
`azimuth`	Counter clock-wise angle in the x-y plane of the right handed Cartesian coordinate system in radians. \(0\) radians are defined in positive x-direction, \(\pi/2\) radians in positive y-direction and so on (\(-\infty\) < azimuth < \(\infty\), \(2\pi\)-cyclic).
`colatitude`	Angle in the x-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians colatitude are defined in positive z-direction, \(\pi/2\) radians in positive x-direction, and \(\pi\) in negative z-direction (\(0\leq\) colatitude \(\leq\pi\)). The colatitude is a variation of the elevation angle.
`elevation`	Angle in the x-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians elevation are defined in positive x-direction, \(\pi/2\) radians in positive z-direction, and \(-\pi/2\) in negative z-direction (\(-\pi/2\leq\) elevation \(\leq\pi/2\)). The elevation is a variation of the colatitude.
`lateral`	Counter clock-wise angle in the x-y plane of the right handed Cartesian coordinate system in radians. \(0\) radians are defined in positive x-direction, \(\pi/2\) radians in positive y-direction and \(-\pi/2\) in negative y-direction (\(-\pi/2\leq\) lateral \(\leq\pi/2\)).
`polar`	Angle in the x-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians polar angle are defined in positive x-direction, \(\pi/2\) radians in positive z-direction, \(\pi\) in negative x-direction and so on (\(-\infty\) < polar < \(\infty\), \(2\pi\)-cyclic).
`frontal`	Angle in the y-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians frontal angle are defined in positive y-direction, \(\pi/2\) radians in positive z-direction, \(\pi\) in negative y-direction and so on (\(-\infty\) < frontal < \(\infty\), \(2\pi\)-cyclic).
`upper`	Angle in the x-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians upper angle are defined in positive x-direction, \(\pi/2\) radians in positive z-direction, and \(\pi\) in negative x-direction (\(0\leq\) upper \(\leq\pi\)).
`radius`	Distance to the origin of the right handed Cartesian coordinate system in meters (\(0\) < radius < \(\infty\)).
`rho`	Radial distance to the the z-axis of the right handed Cartesian coordinate system (\(0\) < rho < \(\infty\)).

Classes:

Coordinates([x, y, z, weights, comment])

Create a Coordinates class object from a set of points in the right-handed cartesian coordinate system.

Functions:

`cart2cyl`(x, y, z)	Transforms from Cartesian to cylindrical coordinates.
`cart2sph`(x, y, z)	Transforms from Cartesian to spherical coordinates.
`cyl2cart`(azimuth, height, radius)	Transforms from cylindrical to Cartesian coordinates.
`sph2cart`(azimuth, colatitude, radius)	Transforms from spherical to Cartesian coordinates.

`cross`(a, b)	Cross product of two Coordinates objects.
`deg2rad`(coordinates[, domain])	Convert a copy of coordinates in degree to radians.
`dot`(a, b)	Dot product of two Coordinates objects.
`rad2deg`(coordinates[, domain])	Convert a copy of coordinates in radians to degree.

class pyfar.Coordinates(x: array = array([], dtype=float64), y: array = array([], dtype=float64), z: array = array([], dtype=float64), weights: array = None, comment: str = '')[source]#

Create a Coordinates class object from a set of points in the right-handed cartesian coordinate system. See see Coordinate Systems and Coordinates for more information.

If you want to initialize in another domain use from_spherical_colatitude, from_spherical_elevation, from_spherical_front, from_spherical_side, or from_cylindrical instead. For conversions from or into degree use deg2rad and rad2deg.

Parameters:

x (ndarray, number) – X coordinate of a right handed Cartesian coordinate system in meters (\(-\infty\) < x < \(\infty\)).
y (ndarray, number) – Y coordinate of a right handed Cartesian coordinate system in meters (\(-\infty\) < y < \(\infty\)).
z (ndarray, number) – Z coordinate of a right handed Cartesian coordinate system in meters (\(-\infty\) < z < \(\infty\)).
weights (array like, number, optional) – Weighting factors for coordinate points. The shape of the array must match the shape of the individual coordinate arrays. The default is None.
comment (str, optional) – Comment about the stored coordinate points. The default is "", which initializes an empty string.

Attributes:

`azimuth`	Counter clock-wise angle in the x-y plane of the right handed Cartesian coordinate system in radians.
`cartesian`	Returns `x`, `y`, `z`.
`cdim`	Return channel dimension.
`colatitude`	Angle in the x-z plane of the right handed Cartesian coordinate system in radians.
`comment`	Get comment.
`cshape`	Return channel shape.
`csize`	Return channel size.
`cylindrical`	Cylindrical coordinates.
`elevation`	Angle in the x-z plane of the right handed Cartesian coordinate system in radians.
`frontal`	Angle in the y-z plane of the right handed Cartesian coordinate system in radians.
`lateral`	Counter clock-wise angle in the x-y plane of the right handed Cartesian coordinate system in radians.
`polar`	Angle in the x-z plane of the right handed Cartesian coordinate system in radians.
`radius`	Distance to the origin of the right handed Cartesian coordinate system in meters (\(0\) < radius < \(\infty\)).
`rho`	Radial distance to the the z-axis of the right handed Cartesian coordinate system (\(0\) < rho < \(\infty\)).
`spherical_colatitude`	Spherical coordinates according to the top pole colatitude coordinate system.
`spherical_elevation`	Spherical coordinates according to the top pole elevation coordinate system.
`spherical_front`	Spherical coordinates according to the frontal pole coordinate system.
`spherical_side`	Spherical coordinates according to the side pole coordinate system.
`upper`	Angle in the x-z plane of the right handed Cartesian coordinate system in radians.
`weights`	Get sampling weights.
`x`	X coordinate of a right handed Cartesian coordinate system in meters (\(-\infty\) < x < \(\infty\)).
`y`	Y coordinate of a right handed Cartesian coordinate system in meters (\(-\infty\) < y < \(\infty\)).
`z`	Z coordinate of a right handed Cartesian coordinate system in meters (\(-\infty\) < z < \(\infty\)).

Methods:

`copy`()	Return a deep copy of the Coordinates object.
`find_nearest`(find[, k, distance_measure, ...])	Find the k nearest coordinates points.
`find_within`(find[, distance, ...])	Find coordinates within a certain distance to the query points.
`from_cartesian`(x, y, z[, weights, comment])	Create a Coordinates class object from a set of points in the right-handed cartesian coordinate system.
`from_cylindrical`(azimuth, z, rho[, weights, ...])	Create a Coordinates class object from a set of points in the cylindrical coordinate system.
`from_spherical_colatitude`(azimuth, ...[, ...])	Create a Coordinates class object from a set of points in the spherical coordinate system.
`from_spherical_elevation`(azimuth, elevation, ...)	Create a Coordinates class object from a set of points in the spherical coordinate system.
`from_spherical_front`(frontal, upper, radius)	Create a Coordinates class object from a set of points in the spherical coordinate system.
`from_spherical_side`(lateral, polar, radius)	Create a Coordinates class object from a set of points in the spherical coordinate system.
`rotate`(rotation[, value, degrees, inverse])	Rotate points stored in the object around the origin of coordinates.
`show`([mask])	Show a scatter plot of the coordinate points.

property azimuth#: Counter clock-wise angle in the x-y plane of the right handed Cartesian coordinate system in radians. \(0\) radians are defined in positive x-direction, \(\pi/2\) radians in positive y-direction and so on (\(-\infty\) < azimuth < \(\infty\), \(2\pi\)-cyclic).

property cartesian#: Returns x, y, z. Right handed cartesian coordinate system. See see Coordinate Systems and Coordinates for more information.

property cdim#

Return channel dimension.

The channel dimension gives the number of dimensions of the coordinate points excluding the last dimension.

property colatitude#: Angle in the x-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians colatitude are defined in positive z-direction, \(\pi/2\) radians in positive x-direction, and \(\pi\) in negative z-direction (\(0\leq\) colatitude \(\leq\pi\)). The colatitude is a variation of the elevation angle.

property comment#: Get comment.

copy()[source]#: Return a deep copy of the Coordinates object.

property cshape#

Return channel shape.

The channel shape gives the shape of the coordinate points excluding the last dimension, which is always 3.

property csize#

Return channel size.

The channel size gives the number of points stored in the coordinates object.

property cylindrical#: Cylindrical coordinates. Returns azimuth, z, rho. See see Coordinate Systems and Coordinates for more information.

property elevation#: Angle in the x-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians elevation are defined in positive x-direction, \(\pi/2\) radians in positive z-direction, and \(-\pi/2\) in negative z-direction (\(-\pi/2\leq\) elevation \(\leq\pi/2\)). The elevation is a variation of the colatitude.

find_nearest(find, k=1, distance_measure='euclidean', radius_tol=None)[source]#

Find the k nearest coordinates points.

Parameters:

find (pf.Coordinates) – Coordinates to which the nearest neighbors are searched.
k (int, optional) – Number of points to return. k must be > 0. The default is 1.
distance_measure (string, optional) –

'euclidean'
distance is determined by the euclidean distance. This is default.

'spherical_radians'
distance is determined by the great-circle distance expressed in radians.

'spherical_meter'
distance is determined by the great-circle distance expressed in meters.
radius_tol (float, None) – For all spherical distance measures, the coordinates must be on a sphere, so the radius must be constant. This parameter defines the maximum allowed difference within the radii. Note that increasing the tolerance decreases the accuracy of the search. The default None uses a tolerance of two times the decimal resolution, which is determined from the data type of the coordinate points using numpy.finfo.

Returns:

index (tuple of arrays) – Indices of the neighbors. Arrays of shape (k, find.cshape) if k>1 else (find.cshape, ).
distance (numpy array of floats) – Distance between the points, after the given distance_measure. It’s of shape (k, find.cshape).

Notes

This is a wrapper for scipy.spatial.cKDTree.

Examples

Find frontal point from a spherical coordinate system

>>> import pyfar as pf
>>> import numpy as np
>>> coords = pf.Coordinates.from_spherical_elevation(
>>>     np.arange(0, 360, 10)*np.pi/180, 0, 1)
>>> to_find = pf.Coordinates(1, 0, 0)
>>> index, distance = coords.find_nearest(to_find)
>>> ax = coords.show(index)
>>> distance
0.0

(Source code, png, hires.png, pdf)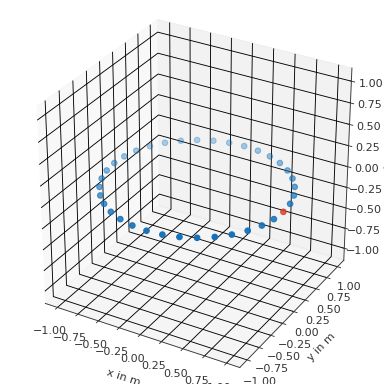

Find multidimensional points in multidimensional coordinates with k=1

>>> import pyfar as pf
>>> import numpy as np
>>> coords = pf.Coordinates(np.arange(9).reshape((3, 3)), 0, 1)
>>> to_find = pf.Coordinates(
>>>     np.array([[0, 1], [2, 3]]), 0, 1)
>>> i, d = coords.find_nearest(to_find)
>>> coords[i] == find
True
>>> i
(array([[0, 0],
        [0, 1]], dtype=int64),
 array([[0, 1],
        [2, 0]], dtype=int64))
>>> d
array([[0., 0.],
       [0., 0.]])

Find multidimensional points in multidimensional coordinates with k=3

>>> import pyfar as pf
>>> import numpy as np
>>> coords = pf.Coordinates(np.arange(9).reshape((3, 3)), 0, 1)
>>> find = pf.Coordinates(
>>>     np.array([[0, 1], [2, 3]]), 0, 1)
>>> i, d = coords.find_nearest(find, 3)
>>> # the k-th dimension is at the end
>>> i[0].shape
(3, 2, 2)
>>> # now just access the k=0 dimension
>>> coords[i][0].cartesian
array([[[0., 0., 1.],
        [1., 0., 1.]],
       [[2., 0., 1.],
        [3., 0., 1.]]])

find_within(find, distance=0.0, distance_measure='euclidean', atol=None, return_sorted=True, radius_tol=None)[source]#

Find coordinates within a certain distance to the query points.

Parameters:

find (pf.Coordinates) – Coordinates to which the nearest neighbors are searched.
distance (number, optional) – Maximum allowed distance to the given points find. Distance must be >= 0. For just exact matches use 0. The default is 0.
distance_measure (string, optional) –

'euclidean'
distance is determined by the euclidean distance. This is default.

'spherical_radians'
distance is determined by the great-circle distance expressed in radians.

'spherical_meter'
distance is determined by the great-circle distance expressed in meters.
atol (float, None) – Absolute tolerance for distance. The default None uses a tolerance of two times the decimal resolution, which is determined from the data type of the coordinate points using numpy.finfo.
return_sorted (bool, optional) – Sorts returned indices if True and does not sort them if False. The default is True.
radius_tol (float, None) – For all spherical distance measures, the coordinates must be on a sphere, so the radius must be constant. This parameter defines the maximum allowed difference within the radii. Note that increasing the tolerance decreases the accuracy of the search, i.e., points that are within the search distance might not be found or points outside the search distance may be returned. The default None uses a tolerance of two times the decimal resolution, which is determined from the data type of the coordinate points using numpy.finfo.

Returns:

index – Indices of the containing coordinates. Arrays of shape (find.cshape).

Return type:

tuple of array

Notes

This is a wrapper for scipy.spatial.cKDTree. Compared to previous implementations, it supports self.ndim>1 as well.

Examples

Find all point with 0.2 m distance from the frontal point

>>> import pyfar as pf
>>> import numpy as np
>>> coords = pf.Coordinates.from_spherical_elevation(
>>>     np.arange(0, 360, 5)*np.pi/180, 0, 1)
>>> find = pf.Coordinates(.2, 0, 0)
>>> index = coords.find_within(find, 1)
>>> coords.show(index)

(Source code, png, hires.png, pdf)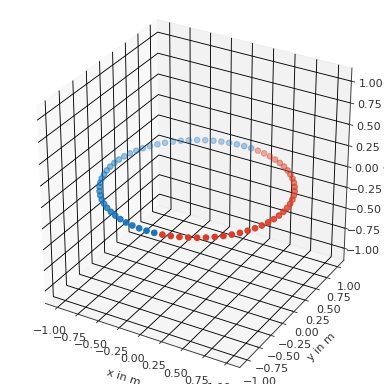

Find all point with 1m distance from two points

>>> import pyfar as pf
>>> coords = pf.Coordinates(np.arange(6), 0, 0)
>>> find = pf.Coordinates([2, 3], 0, 0)
>>> index = coords.find_within(find, 1)
>>> coords.show(index[0])

(Source code, png, hires.png, pdf)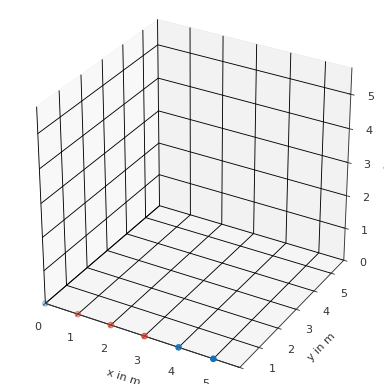

classmethod from_cartesian(x, y, z, weights: array = None, comment: str = '')[source]#

Create a Coordinates class object from a set of points in the right-handed cartesian coordinate system. See see Coordinate Systems and Coordinates for more information.

Parameters:

x (ndarray, number) – X coordinate of a right handed Cartesian coordinate system in meters (\(-\infty\) < x < \(\infty\)).
y (ndarray, number) – Y coordinate of a right handed Cartesian coordinate system in meters ():math:-infty < y < \(\infty\)).
z (ndarray, number) – Z coordinate of a right handed Cartesian coordinate system in meters (\(-\infty\) < z < \(\infty\)).
weights (array like, number, optional) – Weighting factors for coordinate points. The shape of the array must match the shape of the individual coordinate arrays. The default is None.
comment (str, optional) – Comment about the stored coordinate points. The default is "", which initializes an empty string.

Examples

Create a coordinates object

>>> import pyfar as pf
>>> coordinates = pf.Coordinates.from_cartesian(0, 0, 1)

Or the using init

>>> import pyfar as pf
>>> coordinates = pf.Coordinates(0, 0, 1)

classmethod from_cylindrical(azimuth, z, rho, weights: array = None, comment: str = '')[source]#

Create a Coordinates class object from a set of points in the cylindrical coordinate system. See see Coordinate Systems and Coordinates for more information.

Parameters:

azimuth (ndarray, double) – Angle in radiant of rotation from the x-y-plane facing towards positive x direction. Used for spherical and cylindrical coordinate systems.
z (ndarray, double) – The z coordinate
rho (ndarray, double) – Distance to origin for each point in the x-y-plane. Used for cylindrical coordinate systems.
weights (array like, number, optional) – Weighting factors for coordinate points. The shape of the array must match the shape of the individual coordinate arrays. The default is None.
comment (str, optional) – Comment about the stored coordinate points. The default is "", which initializes an empty string.

Examples

Create a coordinates object

>>> import pyfar as pf
>>> coordinates = pf.Coordinates.from_cylindrical(0, 0, 1)

classmethod from_spherical_colatitude(azimuth, colatitude, radius, weights: array = None, comment: str = '')[source]#

Create a Coordinates class object from a set of points in the spherical coordinate system. See see Coordinate Systems and Coordinates for more information.

Parameters:

azimuth (ndarray, double) – Angle in radiant of rotation from the x-y-plane facing towards positive x direction. Used for spherical and cylindrical coordinate systems.
colatitude (ndarray, double) – Angle in radiant with respect to polar axis (z-axis). Used for spherical coordinate systems.
radius (ndarray, double) – Distance to origin for each point. Used for spherical coordinate systems.
weights (array like, number, optional) – Weighting factors for coordinate points. The shape of the array must match the shape of the individual coordinate arrays. The default is None.
comment (str, optional) – Comment about the stored coordinate points. The default is "", which initializes an empty string.

Examples

Create a coordinates object

>>> import pyfar as pf
>>> coordinates = pf.Coordinates.from_spherical_colatitude(0, 0, 1)

classmethod from_spherical_elevation(azimuth, elevation, radius, weights: array = None, comment: str = '')[source]#

Create a Coordinates class object from a set of points in the spherical coordinate system. See see Coordinate Systems and Coordinates for more information.

Parameters:

azimuth (ndarray, double) – Angle in radiant of rotation from the x-y-plane facing towards positive x direction. Used for spherical and cylindrical coordinate systems.
elevation (ndarray, double) – Angle in radiant with respect to horizontal plane (x-z-plane). Used for spherical coordinate systems.
radius (ndarray, double) – Distance to origin for each point. Used for spherical coordinate systems.
weights (array like, float, None, optional) – Weighting factors for coordinate points. The shape of the array must match the shape of the individual coordinate arrays. The default is None.
comment (str, optional) – Comment about the stored coordinate points. The default is "", which initializes an empty string.

Examples

Create a coordinates object

>>> import pyfar as pf
>>> coordinates = pf.Coordinates.from_spherical_elevation(0, 0, 1)

classmethod from_spherical_front(frontal, upper, radius, weights: array = None, comment: str = '')[source]#

Create a Coordinates class object from a set of points in the spherical coordinate system. See see Coordinate Systems and Coordinates for more information.

Parameters:

frontal (ndarray, double) – Angle in radiant of rotation from the y-z-plane facing towards positive y direction. Used for spherical coordinate systems.
upper (ndarray, double) – Angle in radiant with respect to polar axis (x-axis). Used for spherical coordinate systems.
radius (ndarray, double) – Distance to origin for each point. Used for spherical coordinate systems.
weights (array like, number, optional) – Weighting factors for coordinate points. The shape of the array must match the shape of the individual coordinate arrays. The default is None.
comment (str, optional) – Comment about the stored coordinate points. The default is "", which initializes an empty string.

Examples

Create a coordinates object

>>> import pyfar as pf
>>> coordinates = pf.Coordinates.from_spherical_front(0, 0, 1)

classmethod from_spherical_side(lateral, polar, radius, weights: array = None, comment: str = '')[source]#

Create a Coordinates class object from a set of points in the spherical coordinate system. See see Coordinate Systems and Coordinates for more information.

Parameters:

lateral (ndarray, double) – Angle in radiant with respect to horizontal plane (x-y-plane). Used for spherical coordinate systems.
polar (ndarray, double) – Angle in radiant of rotation from the x-z-plane facing towards positive x direction. Used for spherical coordinate systems.
radius (ndarray, double) – Distance to origin for each point. Used for spherical coordinate systems.
weights (array like, number, optional) – Weighting factors for coordinate points. The shape of the array must match the shape of the individual coordinate arrays. The default is None.
comment (str, optional) – Comment about the stored coordinate points. The default is "", which initializes an empty string.

Examples

Create a coordinates object

>>> import pyfar as pf
>>> coordinates = pf.Coordinates.from_spherical_side(0, 0, 1)

property frontal#: Angle in the y-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians frontal angle are defined in positive y-direction, \(\pi/2\) radians in positive z-direction, \(\pi\) in negative y-direction and so on (\(-\infty\) < frontal < \(\infty\), \(2\pi\)-cyclic).

property lateral#: Counter clock-wise angle in the x-y plane of the right handed Cartesian coordinate system in radians. \(0\) radians are defined in positive x-direction, \(\pi/2\) radians in positive y-direction and \(-\pi/2\) in negative y-direction (\(-\pi/2\leq\) lateral \(\leq\pi/2\)).

property polar#: Angle in the x-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians polar angle are defined in positive x-direction, \(\pi/2\) radians in positive z-direction, \(\pi\) in negative x-direction and so on (\(-\infty\) < polar < \(\infty\), \(2\pi\)-cyclic).

property radius#: Distance to the origin of the right handed Cartesian coordinate system in meters (\(0\) < radius < \(\infty\)).

property rho#: Radial distance to the the z-axis of the right handed Cartesian coordinate system (\(0\) < rho < \(\infty\)).

rotate(rotation: str, value=None, degrees=True, inverse=False)[source]#

Rotate points stored in the object around the origin of coordinates.

This is a wrapper for scipy.spatial.transform.Rotation (see this class for more detailed information).

Parameters:

rotation (str) –

'quat'
Rotation given by quaternions.

'matrix'
Rotation given by matrixes.

'rotvec'
Rotation using rotation vectors.

'xyz'
Rotation using euler angles. Up to three letters. E.g., 'x' will rotate about the x-axis only, while 'xz' will rotate about the x-axis and then about the z-axis. Use lower letters for extrinsic rotations (rotations about the axes of the original coordinate system xyz, which remains motionless) and upper letters for intrinsic rotations (rotations about the axes of the rotating coordinate system XYZ, solidary with the moving body, which changes its orientation after each elemental rotation).
value (number, array like) – Amount of rotation in the format specified by rotation (see above).
degrees (bool, optional) – Pass angles in degrees if using 'rotvec' or euler angles ('xyz'). The default is True. Use False to pass angles in radians.
inverse (bool, optional) – Apply inverse rotation. The default is False.

Notes

Points are converted to the cartesian right handed coordinate system for the rotation.

Examples

Get a coordinates object

>>> import pyfar as pf
>>> coords = pf.Coordinates(np.arange(-5, 5), 0, 0)

Rotate 45 degrees about the y-axis using

quaternions

>>> coordinates.rotate('quat', [0 , 0.38268343, 0 , 0.92387953])

a rotation matrix

>>> coordinates.rotate('matrix',
...    [[ 0.70710678,  0 ,  0.70710678],
...     [ 0         ,  1 ,  0.        ],
...     [-0.70710678,  0 ,  0.70710678]])

a rotation vector

>>> coordinates.rotate('rotvec', [0, 45, 0])

euler angles

>>> coordinates.rotate('XYZ', [0, 45, 0])

To see the result of the rotation use

>>> coordinates.show()

show(mask=None, **kwargs)[source]#

Show a scatter plot of the coordinate points.

Parameters:

mask (boolean numpy array, None, optional) – Mask or indexes to highlight. Highlight points in red if mask==True. The default is None, which plots all points in the same color.
kwargs (optional) – Keyword arguments are passed to matplotlib.pyplot.scatter. If a mask is provided and the key c is contained in kwargs, it will be overwritten.

Returns:

ax – The axis used for the plot.

Return type:

Axes3D

property spherical_colatitude#: Spherical coordinates according to the top pole colatitude coordinate system. Returns azimuth, colatitude, radius. See see Coordinate Systems and Coordinates for more information.

property spherical_elevation#: Spherical coordinates according to the top pole elevation coordinate system. azimuth, elevation, radius. See see Coordinate Systems and Coordinates for more information.

property spherical_front#: Spherical coordinates according to the frontal pole coordinate system. Returns frontal, upper, radius. See see Coordinate Systems and Coordinates for more information.

property spherical_side#: Spherical coordinates according to the side pole coordinate system. Returns lateral, polar, radius. See see Coordinate Systems and Coordinates for more information.

property upper#: Angle in the x-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians upper angle are defined in positive x-direction, \(\pi/2\) radians in positive z-direction, and \(\pi\) in negative x-direction (\(0\leq\) upper \(\leq\pi\)).

property weights#: Get sampling weights.

property x#: X coordinate of a right handed Cartesian coordinate system in meters (\(-\infty\) < x < \(\infty\)).

property y#: Y coordinate of a right handed Cartesian coordinate system in meters (\(-\infty\) < y < \(\infty\)).

property z#: Z coordinate of a right handed Cartesian coordinate system in meters (\(-\infty\) < z < \(\infty\)).

pyfar.classes.coordinates.cart2cyl(x, y, z)[source]#

Transforms from Cartesian to cylindrical coordinates.

Cylindrical coordinates follow the convention that the azimuth is 0 at positive x-direction and pi/2 at positive y-direction (counter clockwise rotation). The height is identical to the z-coordinate and the radius is measured orthogonal from the z-axis.

Cartesian coordinates follow the right hand rule.

\[ \begin{align}\begin{aligned}azimuth &= \arctan(\frac{y}{x}),\\height &= z,\\radius &= \sqrt{x^2 + y^2},\end{aligned}\end{align} \]

\[0 < azimuth < 2 \pi\]

Parameters:

x (numpy array, number) – X values
y (numpy array, number) – Y values
z (numpy array, number) – Z values

Returns:

azimuth (numpy array, number) – Azimuth values
height (numpy array, number) – Height values
radius (numpy array, number) – Radii

Notes

To ensure proper handling of the azimuth angle, the numpy.arctan2 implementation from numpy is used.

pyfar.classes.coordinates.cart2sph(x, y, z)[source]#

Transforms from Cartesian to spherical coordinates.

Spherical coordinates follow the common convention in Physics/Mathematics. The colatitude is measured downwards from the z-axis and is 0 at the North Pole and pi at the South Pole. The azimuth is 0 at positive x-direction and pi/2 at positive y-direction (counter clockwise rotation).

Cartesian coordinates follow the right hand rule.

\[ \begin{align}\begin{aligned}azimuth &= \arctan(\frac{y}{x}),\\colatitude &= \arccos(\frac{z}{r}),\\radius &= \sqrt{x^2 + y^2 + z^2}\end{aligned}\end{align} \]

\[ \begin{align}\begin{aligned}0 < azimuth < 2 \pi,\\0 < colatitude < \pi\end{aligned}\end{align} \]

Parameters:

x (numpy array, number) – X values
y (numpy array, number) – Y values
z (numpy array, number) – Z values

Returns:

azimuth (numpy array, number) – Azimuth values
colatitude (numpy array, number) – Colatitude values
radius (numpy array, number) – Radii

Notes

To ensure proper handling of the azimuth angle, the numpy.arctan2 implementation from numpy is used.

pyfar.cross(a, b)[source]#

Cross product of two Coordinates objects.

\[\vec{a} \times \vec{b} = (a_y \cdot b_z - a_z \cdot b_y) \cdot \hat{x} + (a_z \cdot b_x - a_x \cdot b_z) \cdot \hat{y} + (a_x \cdot b_y - a_y \cdot b_x) \cdot \hat{z}\]

Parameters:

a (pf.Coordinates) – first argument, must be broadcastable with b
b (pf.Coordinates) – second argument, much be broadcastable with a

Returns:

result – new Coordinates object with the cross product of the two objects

Return type:

pf.Coordinates

Examples

>>> import pyfar as pf
>>> a = pf.Coordinates(1, 0, 0)
>>> b = pf.Coordinates(0, 1, 0)
>>> result = pf.cross(a, b)
>>> result.cartesian
array([0., 0., 1.])

pyfar.classes.coordinates.cyl2cart(azimuth, height, radius)[source]#

Transforms from cylindrical to Cartesian coordinates.

Cylindrical coordinates follow the convention that the azimuth is 0 at positive x-direction and pi/2 at positive y-direction (counter clockwise rotation). The height is identical to the z-coordinate and the radius is measured orthogonal from the z-axis.

Cartesian coordinates follow the right hand rule.

\[ \begin{align}\begin{aligned}x &= radius \cdot \cos(azimuth),\\y &= radius \cdot \sin(azimuth),\\z &= height\end{aligned}\end{align} \]

\[0 < azimuth < 2 \pi\]

Parameters:

azimuth (numpy array, number) – Azimuth values
height (numpy array, number) – Height values
radius (numpy array, number) – Radii

Returns:

x (numpy array, number) – X values
y (numpy array, number) – Y values
z (numpy array, number) – Z values

Notes

To ensure proper handling of the azimuth angle, the numpy.arctan2 implementation from numpy is used.

pyfar.deg2rad(coordinates, domain='spherical')[source]#

Convert a copy of coordinates in degree to radians.

Parameters:

coordinates (array like) – N-dimensional array of shape (…, 3).
domain (str, optional) –
Specifies what data are contained in coordinates

'spherical'
Spherical coordinates with angles contained in coordinates[..., 0:2] and radii in coordinates[..., 2]. The radii are ignored during the conversion.

'cylindrical'
Cylindrical coordinates with angles contained in coordinates[..., 0], heights contained in coordinates[..., 1], and radii in coordinates[..., 2]. The heights and radii are ignored during the conversion.

Returns:

coordinates – The converted coordinates of the same shape as the input data.

Return type:

numpy array

pyfar.dot(a, b)[source]#

Dot product of two Coordinates objects.

\[\vec{a} \cdot \vec{b} = a_x \cdot b_x + a_y \cdot b_y + a_z \cdot b_z\]

Parameters:

a (pf.Coordinates) – first argument, must be broadcastable with b
b (pf.Coordinates) – second argument, much be broadcastable with a

Returns:

result – array with the dot product of the two objects

Return type:

np.ndarray

Examples

>>> import pyfar as pf
>>> a = pf.Coordinates(1, 0, 0)
>>> b = pf.Coordinates(1, 0, 0)
>>> pf.dot(a, b)
array([1.])

pyfar.rad2deg(coordinates, domain='spherical')[source]#

Convert a copy of coordinates in radians to degree.

Parameters:

coordinates (array like) – N-dimensional array of shape (…, 3).
domain (str, optional) –
Specifies what data are contained in coordinates

'spherical'
Spherical coordinates with angles contained in coordinates[..., 0:2] and radii in coordinates[..., 2]. The radii are ignored during the conversion.

'cylindrical'
Cylindrical coordinates with angles contained in coordinates[..., 0], heights contained in coordinates[..., 1], and radii in coordinates[..., 2]. The heights and radii are ignored during the conversion.

Returns:

coordinates – The converted coordinates of the same shape as the input data.

Return type:

numpy array

pyfar.classes.coordinates.sph2cart(azimuth, colatitude, radius)[source]#

Transforms from spherical to Cartesian coordinates.

Spherical coordinates follow the common convention in Physics/Mathematics. The colatitude is measured downwards from the z-axis and is 0 at the North Pole and pi at the South Pole. The azimuth is 0 at positive x-direction and pi/2 at positive y-direction (counter clockwise rotation).

Cartesian coordinates follow the right hand rule.

\[ \begin{align}\begin{aligned}x &= radius \cdot \sin(colatitude) \cdot \cos(azimuth),\\y &= radius \cdot \sin(colatitude) \cdot \sin(azimuth),\\z &= radius \cdot \cos(colatitude)\end{aligned}\end{align} \]

\[ \begin{align}\begin{aligned}0 < azimuth < 2 \pi\\0 < colatitude < \pi\end{aligned}\end{align} \]

Parameters:

azimuth (numpy array, number) – Azimuth values
colatitude (numpy array, number) – Colatitude values
radius (numpy array, number) – Radii

Returns:

x (numpy array, number) – X values
y (numpy array, number) – Y values
z (numpy array, number) – Z vales